Kelly Criterion (Position Sizing)
Introduction
This article explores the Kelly Criterion and its application in options trading.
Key Takeaways:
- Kelly Criterion Basics: A mathematical formula for optimal position sizing, balancing risk and reward.
- Practical Application: Utilize trading history to estimate inputs for the formula.
- Risk Management: Advises on the proportion of capital to invest, aiding in risk reduction and optimal compound growth rate.
- Advantages: Maximizes long-term growth while minimizing significant losses.
What is the Kelly Criterion?
Inventor of the Kelly Criterion
The Kelly Criterion was developed by John Larry Kelly Jr., a scientist at Bell Labs. He formulated this criterion in 1956, originally intending it to be used for information theory and telecommunications. Kelly’s work was primarily focused on signal noise issues, but his formula gained more prominence in the field of economics and investment, particularly in risk management and speculative investing.
When applied to investing or trading, it is a formula designed to determine the optimal size of a series of positions in order to maximize wealth over time. In trading, it helps in allocating funds to different investments by balancing the trade-off between risk and return.
Expected Value
The concept of “expected value” is crucial in probabilistic and statistical analyses, especially in gambling and investments. It represents the average outcome of a random event when the process is repeated many times. In finance, the expected value helps investors understand what they can expect to gain or lose on an investment when considering all possible outcomes.
Expected value is calculated by multiplying each possible outcome by the likelihood of that outcome occurring, and then summing all of these values.
This concept is integral to applying the Kelly Criterion, as it relates to assessing the long-term profitability or loss of an investment – like an options trade.
The Kelly Criterion Formula
A more general form of the Kelly formula allows for partial losses, which is relevant for investments and trading. It makes the assumption future probabilities are known.
where:
is the probability that the investment increases in value.
is the probability that the investment decreases in value (
).
is the fraction that is lost in a negative outcome. If the position price falls 10%, then
is the fraction that is gained in a positive outcome. If the position price rises 10%, then
.
is the optimal fraction of your total portfolio to apply to a particular position. This is what we want to know.
Note that the Kelly criterion is valid only for known outcome probabilities, which is not the case with investments. If you are risk averse, or are less certain about any of the variables to the equation, you should not invest the full Kelly fraction.
Lets Play a Game to Illustrate the Kelly Criterion in Action
You have a special coin that lands on heads 60% of the time and tails 40% of the time. You have the advantage of knowing about this special coin in advance and you decide to gamble with a friend using this coin. Knowing in advance how this coin lands as a heads/tails ratio – while your counterparty thinks the heads/tails ratio is 50/50 – is your known alpha.
Easy money right?
These are the Rules to the Game (Your Friend is the Counterparty):
- You start with $25.
- You make even-money bets on your coin that lands on heads 60% of the time.
- You can bet as much as you would like on each flip.
- You get 300 flips to bet on.
- The max you can win in total is capped at $250 (10x). If you reach that amount you are done playing.
Would you play this game? It has a positive expected value. Any rational investor, with a special coin/edge/alpha should want to play this game.
The question is, what amount should you bet on each flip? Your whole account? A fixed amount? A certain percentage of your account?
Kelly Criterion answers this question by providing the optimal position size relative to your account size.
What Most Traders Do (Wrong)
61 people played this game and the results are pretty surprising:
- 28% of the participants went bust – they took a positive expected value edge and went to $0
- The average payout was just $91
- Only 21% of the participants hit the $250.00 max gain cap
- 18 of the 61 participants bet everything on one toss
- Two-thirds gambled on tails at some stage in the experiment
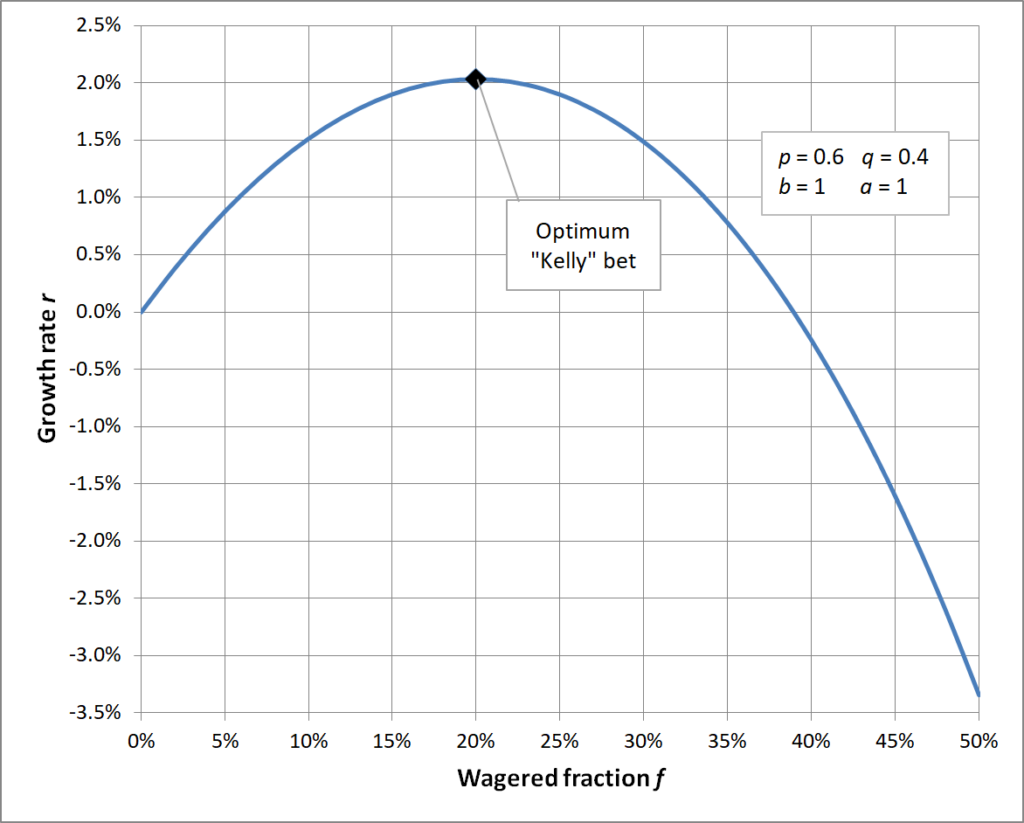
In the given scenario, using the Kelly Criterion formula and considering the specific odds, the optimal strategy would be to bet 20% of the account on each coin toss. This method would yield (over time) an average growth rate of 2.034% per coin flip.
The expected value after 300 rounds works out to $10,505 ($25 ⋅ (1.02034)^300) assuming no $250.00 cap on winnings.
Why did the 61 people perform so poorly in this experiment? They bet the wrong fraction of their account on each flip – most underperform and some end at zero.
Kelly Criterion tells us that the ideal fraction to bet for these inputs is 20%.
Experiment:
- Betting the entire account on each flip is risky. Despite the known advantage, the variability could lead to losing the entire account.
- Betting a large percentage, say 50% is also risky and many potential outcomes end at 0.
- Betting a small percentage, say 5% is less risky and is very likely to lead a positive outcome. However, using this assumption the expected value is not optimized.
- Using Kelly Criterion (betting 20% of the account on each flip), the expected value is maximally positive.
This can be visualized by comparing growth rate to wagered fraction:

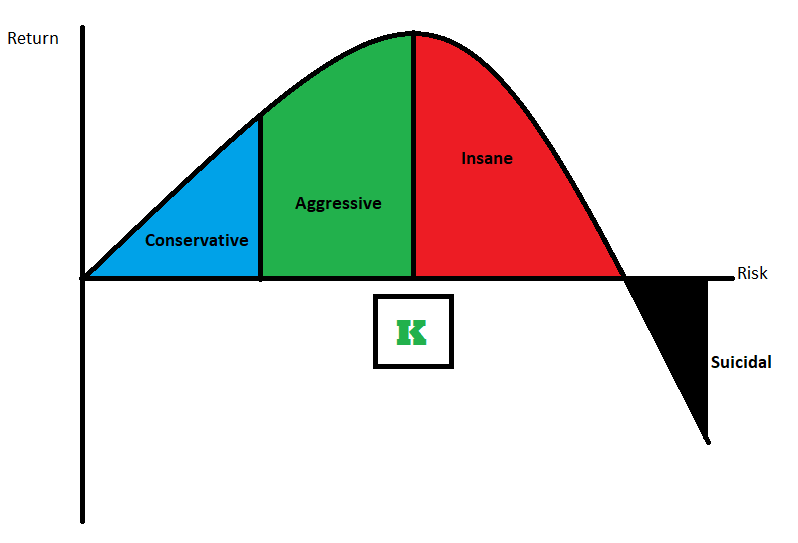
Insight: Bet to much, you likely go to zero, rarely get max return. Bet too little and your compounding growth rate is too low. The peak of this curve is the highest compound growth rate you could expect and is correlated to the optimal “wagered fraction” or position size relative to account size.
Kelly Criterion Application in Options Trading
Determining the Optimal Option Position Size
For options traders, the Kelly Criterion provides a framework to calculate the ideal position size. It considers the probability of a trade’s success, the expected return, and the risk of loss. By inputting these variables, traders can understand how much of their total account should be allocated to a specific trade.
Defined Risk and Trading Debit or Credit Spreads Using Kelly Criterion
In defined risk option spreads, the Kelly Criterion assists in managing risk by suggesting position sizes that prevent the ideal compound growth rate for your entire account. It’s particularly useful in strategies involving selling options, where the potential for loss can sometimes outweigh the profit. For long or short defined risk strategies, the defined risk/reward attributes of the spreads themselves provide the inputs to the Kelly Criterion formula.
Example: XYZ Stock and a Credit Spread
- Scenario: XYZ stock is trading at $100. You’re considering a credit spread by selling the $95 put and buying the $90 put, with 45 days until expiration.
Get Your Inputs :
- p: is the probability that the investment increases in value. This is your “probability of profit” metric provided by brokers.
- q: is 1- p
- a: is your stop loss as a percent of total trade value – or max loss loss as a percent.
- b: is your limit order as a percent of total trade value – or max gain as a percent.
is the optimal position size
By applying this formula, investors can figure out the percentage of their total capital that should be invested in a single trade. This strategy is essential for managing investment risk and optimizing portfolio growth. Remember, you don’t necessarily want winning trades, you want a winning account over a number of trades.
Keeping a journal can help more accurately and easily track trading performance when compared to reconstructing old trades from broker statements to determine a PnL.
Effectively Using the Kelly Criterion in Options Trading:
- Gather Trade Data: Retrieve data on your last 50-60 trades. This can be done through your broker or by reviewing your journal. For those with a systematic trading approach, backtest your system for these results.
- Calculate Win/Loss Probability (p): Calculate by dividing the number of profitable trades by the total number of trades.
- Calculate Win/Loss Profitability as a Percentage(a and b): Calculate this by averaging your average wins and your average losses as a percent of the total trade size.
- Calculate Kelly’s Formula: Input these figures into the Kelly Criterion formula and find the “optimal” position size.
- Trade Using the Kelly Percentage: The output gives you the Kelly percentage, guiding how much of your portfolio to allocate to a trade.
- Update Your Inputs With New Data: Update your inputs with your live trading data going forward to adjust your strategy with the latest optimal position size value.
Utilizing Option “Delta” or Probability of Profit (P.o.P.) as an Approximation of Probability in the Kelly Criterion
- Delta: The delta of an option indicates how much the price of an option is expected to move relative to a $1 move in the underlying stock. It can be used as a proxy for the probability of an option expiring in the money, thus informing the win probability in the Kelly Criterion.
- When trading multi-leg strategies, you have to consider all of the legs to arrive at a “net Delta” value for your option strategy.
- The credit received or debit paid also impacts the “break even” thresholds moving them either further (credits) or closer (debits). Your credit spread can go in the money and the trade can still be profitable. Your debit spread can go in the money and still be unprofitable.
- You must consider all of these factors when making an assumption on profitability of a particular option strategy.
Utilizing Max Profit and Max Loss of a Spread in the Kelly Criterion
- Max Gain and Loss: In a defined risk option spread, your maximum gain is the credit received (or debit paid), and the maximum loss (or gain) is the difference between strike prices minus the credit received (or debit paid).
- If you have stops or limits in your strategy those can be considered when determining these variables. However, if you use stops and limits then you are now changing the probability of wins/losses.
- The easy assumption, and the most accurate would be to assume any spread is held until expiration, until max gain or max loss, or some fraction thereof.
By combining these elements, options traders can more accurately gauge the appropriate position size for a given trade, aligning with their risk tolerance and market outlook. Remember, the Kelly Criterion is a guide, not a guarantee, and should be used as part of a comprehensive trading strategy.
Interpreting the Kelly Criterion also speaks to the importance of diversifying investments efficiently. Meaning, traders might not want to let equity or option positions grow past the optimal size.
Using Trading Journals for Kelly Criterion Analysis
Traders can greatly benefit from analyzing their past trades, as recorded in their trading journals, to determine the necessary variables for the Kelly Criterion analysis. A thorough review of previous trades helps in calculating key metrics like win rate, average win, and average loss. These metrics are essential for accurately applying the Kelly Criterion. The win rate informs the probability of a successful trade, while the average win and loss figures help in determining the win/loss ratio. Consistently tracking and analyzing these variables over time can provide traders with a clearer understanding of their trading performance and assist in making more informed decisions based on the Kelly Criterion.
Advantages and Limitations of the Kelly Criterion
Advantages
The Kelly Criterion offers several advantages for option trading strategies. It provides a systematic approach to determine optimal position sizes, balancing the potential for profit against the risk of loss. This helps in maximizing long-term capital growth while minimizing the risk of significant drawdowns or total account depletion. By using historical data and probabilities from your own trading, the Kelly Criterion guides traders in making more informed, mathematically sound decisions about how much to invest in each position.
- Risk Management: It offers a systematic approach to managing risk.
- Capital Growth: Helps in maximizing capital growth over time by keeping your position size optimized.
- Customization: Can be tailored to individual risk tolerance and trading style.
Limitations
The Kelly Criterion is a mathematical model and, like any system, it’s not flawless. It doesn’t guarantee winning stock picks or market crash predictions, and there’s always an element of uncertainty in the markets. Diversification, as suggested by the model, is about spreading investments across various asset classes to mitigate risks. The primary drawback of the Kelly Criterion is the potential for suggesting large initial investments, which can be risky in the short term. The same formula applies to wagering, with the variables adjusted accordingly. Overall, efficient money management, like that offered by the Kelly Criterion, is crucial for maximizing gains and minimizing losses, though it doesn’t guarantee constant high returns.
- Estimation Accuracy: Relies on accurate estimation of probabilities and returns.
- Market Dynamics: Market changes can affect the assumptions used in the formula.
- Over-Optimism: May lead to over-leveraging if not used cautiously.
Conclusion
The Kelly Criterion is a valuable tool for options traders and those especially involved in trading spreads. It aids in making informed decisions about position sizes, thereby enhancing risk management and potential for capital growth.